Complex Motion and Problem-Solving

Kinematics from a high schooler, Part 2

Alola! Let’s start off right where we left off!

Lesson Three - Definition of Complex Motion

Complex Motion is a type of motion where the object is non-uniformly accelerated; either slowing down or speeding up exponentially.

In this motion, since the object is either slowing down or speeding up exponentially, its position is changing in an exponential form, and its velocity has a very different magnitude throughout the time the motion is occuring. So, the graph that is a straight line depends on the degree of the graph.

For example, if a-t graph is linear, then jerk will be horizontal. If the jerk is linear, then the snap is horizontal.

We cannot determine the equations as the degree (velocity - acc - jerk - snap - crackle, etc.) will make these different and more and more complex. We need calculus to go deeper into higher levels of complex motion

Lesson Four - Strategy for Problem-Solving

We defined uniform motion as a type of motion where the object is moving at a constant speed; neither slowing down nor speeding up. Let’s look at an example.

Scenario: A man walks to the right in uniform motion.

Let’s say the man is moving to the right at a speed of 3 m/s.

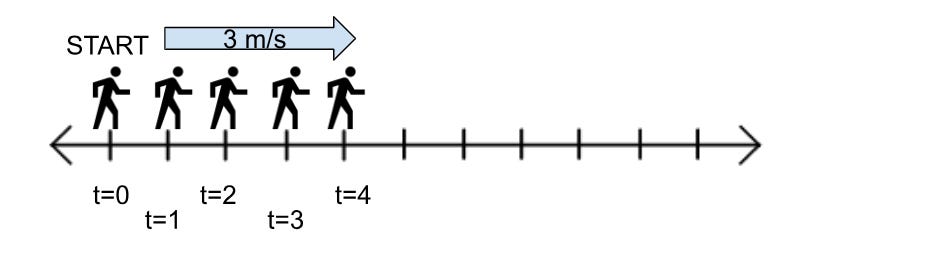
To start off, try to (this is a strobe diagram by the way):

1. Describe the motion in words

   1. The (object) moves right at a constant speed of  (speed) over a period of (time) time. It turns around and moves at (velocity) over a period of (time)... (if relevant)

   2. The man moves at a velocity of 3 m/s right over a period of 4 seconds.

2. Draw a diagram

   1. We can see the man moving along the number line, given to us that he is moving right. Let’s add some symbols to our image to better understand what’s going on and to answer potential questions regarding his movement.

      

   2. I personally prefer drawing a diagram, but it’s important to first understand and picture the problem in your head. This is especially important in non-uniform, but important here as well. 

Then figure out what you know, and what you need to find out! Follow these steps to solve any problem!

Example:

Q: How much distance did the man travel?

1. Always write what you know first before writing any equations.

v? 3m/s right

Δt? 4s

Δd? To find out

2. Then determine the equations to be used

v=Δd/Δt

You can either plug in the values in v=Δd/Δt or solve for Δd and then plug it in.

E.g.

v=Δd/Δt

Δd=vΔt

3. Plug in the values with units

Δd=vΔt

Δd=3m/s*4s

Δd=12m

4. Check if the answer makes sense, both with unit math and logical derivation

Our answer is 12m. We wanted Δd. So, we wanted displacement, which is a vector. We need to submit our answer with a direction!

The units are acceptable. In m/s * s, the s cancels so we are left with m.

5. Clearly box the answer

This is actually a very underrated step. Psychologists actually conducted a study where students who boxed their answer caught a mistake 15% more frequently while they were boxing the answer rather than students who just left it unclear. This gives you a few seconds to briefly look at your work and overview Step 4.

Ans: 12m right of the starting point

And BOOM! That’s all you need to know for how to solve problems. Although a very simple example, this strategy actually works with all problems, no matter how complicated! The best advice, no matter how hard the problem, is to take it step by step.

Try these extra practice questions if you’re feeling extra spicy and submit them in the [comments]

Great! Understanding so far? Next time, we will do a step-by-step for a non-uniform motion problem, plus an included v-t and a-t graph!!!!!!

Sayonara!